Students explore the relationship between input and output values and learn to use algebraic expressions and equations.

This Nrich problem gives practice in calculating with fractions and encourages different ways of representing and recording.

This question examines the algebraic equations for three different spheres. The intersections of each pair of spheres are then studied, both using the equations and thinking about the geometry of the spheres. For two spheres where one is not contained inside of the other there are three possibilities for how they intersect.

This lesson unit is intended to help teachers assess how well students are able to identify linear and quadratic relationships in a realistic context: the number of tiles of different types that are needed for a range of square tabletops. In particular, this unit aims to identify and help students who have difficulties with: choosing an appropriate, systematic way to collect and organize data; examining the data and looking for patterns; finding invariance and covariance in the numbers of different types of tile; generalizing using numerical, geometrical or algebraic structure; and describing and explaining findings clearly and effectively.

This lesson unit is intended to help you assess how well students working with square numbers are able to: choose an appropriate, systematic way to collect and organize data, examining the data for patterns; describe and explain findings clearly and effectively; generalize using numerical, geometrical, graphical and/or algebraic structure; and explain why certain results are possible/impossible, moving towards a proof.

In this module, students explore and experience the utility of analyzing algebra and geometry challenges through the framework of coordinates. The module opens with a modeling challenge, one that reoccurs throughout the lessons, to use coordinate geometry to program the motion of a robot that is bound within a certain polygonal region of the plane—the room in which it sits. To set the stage for complex work in analytic geometry (computing coordinates of points of intersection of lines and line segments or the coordinates of points that divide given segments in specific length ratios, and so on), students will describe the region via systems of algebraic inequalities and work to constrain the robot motion along line segments within the region.

Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.

This Nrich problem is an accessible context in which pupils can apply their knowledge of number properties. It provides a great opportunity for learners to reason logically and to communicate their reasoning with others.

In this lesson designed to enhance literacy skills, students learn how to read and interpret a distance–time graph.

Students learn about an important characteristic of lines: their slopes. Slope can be determined either in graphical or algebraic form. Slope can also be described as positive, negative, zero or undefined. Students get an explanation of when and how these different types of slope occur. Finally, they learn how slope relates to parallel and perpendicular lines. When two lines are parallel, they have the same slope and when they are perpendicular their slopes are negative reciprocals of one another.

Students learn about an important characteristic of lines: their slopes. Slope can be determined either in graphical or algebraic form. Slope can also be described as positive, negative, zero or undefined. Students get an explanation of when and how these different types of slope occur. Finally, they learn how slope relates to parallel and perpendicular lines. When two lines are parallel, they have the same slope and when they are perpendicular their slopes are negative reciprocals of one another.

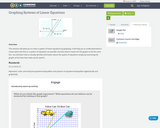
This seminar will allow you to solve a system of linear equations by graphing. It will help you to understand what it means when the lines in a system of equations are parallel, and also what it means for the graphs to be the same line. You will learn how to visually identify information about the system of equations simply by examining the graphs of the lines that make up the system.StandardsCC.2.2.HS.D.10Represent, solve, and interpret equations/inequalities and systems of equations/inequalities algebraically and graphically.

This exploration can be done in class near the beginning of a unit on graphing parabolas. Students need to be familiar with intercepts, and need to know what the vertex is.

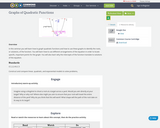
In this seminar you will learn how to graph quadratic functions and how to use these graphs to identify the roots, or solutions, of the function. You will learn how to use different arrangements of the equation in order to locate specific, important points for the graph. You will also learn why the intercepts of the function translate to solutions of the equation. Standards CC.2.2.HS.C.5 Construct and compare linear, quadratic, and exponential models to solve problems,

This Nrich problem follows on from Keep It Simple and Egyptian Fractions
These three problems together offer students an opportunity to engage with some mathematical ideas in depth and not just with the rather mechanical process of adding and subtracting fractions.

This problem in particular requires students to compare fractions and may deepen their understanding of their relative sizes.

This Nrich problem requires children to apply their knowledge of factors and multiples, and is a good way of making the link between sharing, division and multiples/factors. It may also be used to introduce learners to the fact that a problem can have more than one solution and that the solutions can be generalized. It can be approached in many different ways so can be a useful context in which to talk about different ways of recording and different methods of solving problems.

This task is designed to make students think about the meaning of the quantities presented in the context and choose which ones are appropriate for the two different constraints presented. In particular, note that the purpose of the task is to have students generate the constraint equations for each part (though the problem statements avoid using this particular terminology), and not to have students solve said equations.

This problem asks the students to represent a sequence of operations using an expression and then to write and solve simple equations. The problem is posed as a game and allows the students to visualize mathematical operations. It would make sense to actually play a similar game in pairs first and then ask the students to record the operations to figure out each other's numbers.

This Nrich task is a group activity or game. Students work to discover a rule by working together to evaluate patterns.

This is a community contributed High School Equivalency Algebra textbook, focused on algebra material for the GED(R) math test. Use as is, or download and modify to your heart's content. Covers integers to functions.

This Nrich problem provides a fraction-based challenge for students who already possess a good understanding of fraction addition and subtraction, and it leads to algebraic manipulation of that same process.