In this Nrich activity students explore patterns with numbers in a square. This activity encourages multiple responses, creativity, discourse, and number sense.

This Nrich problem can be used to introduce learning about percentage increases and decreases.

Code-breaking is often about partial conclusions gradually adding up to possibilities. This problem is unlikely to be done instantly by most students, so discussion should bring up lots of helpful thoughts to share around a group, energizing explanation and stimulating individuals into new reasoning and strategy.

Students apply and interpret their understanding of area in a real world situation.

In this Nrich problem students build on their existing knowledge of proportions to build a function in an engaging context.

In this guide you will find eleven terms and definitions for Computational Thinking (CT) concepts. These concepts can be incorporated into existing lesson plans, projects, and demonstrations in order to infuse CT into any disciplinary subject.

The original copy of this information was created by Google and shared at https://docs.google.com/document/d/1i0wg-BMG3TdwsShAyH_0Z1xpFnpVcMvpYJceHGWex_c/edit. The only change made has been the format of the document. All information is exactly the same.

Countdown Fractions in this Nrich game offers a motivating context in which to practice calculating with fractions. There is usually more than one way of hitting the target, which offers an opportunity for rich discussion on the merits of alternative methods.

This Nrich activity, in line with the theme for this month, offers an 'action' to perform on a group of numbers which pupils can continue and explore. Or, you could think of the writing down of the 'description' of a sequence as an action performed on that sequence. It might particularly appeal to those pupils who enjoy number work but who are perhaps not used to succeeding in this area.

This Nrich interactive environment can be used with students, perhaps on an interactive whiteboard, for many different purposes. These might include, for example, exploring ideas associated with factors and multiples, or addition and subtraction. It is also an ideal context in which to investigate fractions and ratio, or to look at finding combinations.

This Nrich problem is intentionally difficult as it stands, but this allows us to focus on promoting resilience and perseverance with children.

This problem was designed to explore equivalence of change (ie. if a 10% decrease isn't the opposite of a 10% increase, what is? ) and to move students towards the concept: exponential growth and decay.

'Tricks' tap into children's natural curiosity and can provide the motivation for exploring the underlying mathematics in order to unpick how they are done. This Nrich problem explores a "trick" to provide an engaging context in which to explore place value and in particular 'adding nine' as 'adding ten and subtracting one'.

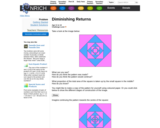
The Nrich problem offers opportunities to think about area, proportion and fractions, while offering an informal introduction to the mathematics of infinity and convergence which would not normally be met by younger students, to tempt their curiosity.

Students discover the mathematical constant phi, the golden ratio, through hands-on activities. They measure dimensions of "natural objects"—a star, a nautilus shell and human hand bones—and calculate ratios of the measured values, which are close to phi. Then students learn a basic definition of a mathematical sequence, specifically the Fibonacci sequence. By taking ratios of successive terms of the sequence, they find numbers close to phi. They solve a squares puzzle that creates an approximate Fibonacci spiral. Finally, the instructor demonstrates the rule of the Fibonacci sequence via a LEGO® MINDSTORMS® NXT robot equipped with a pen. The robot (already created as part of the companion activity, The Fibonacci Sequence & Robots) draws a Fibonacci spiral that is similar to the nautilus shape.

This Nrich problem gives learners practice in fractions (tenths) as well as in addition and subtraction in a challenging form.

This Nrich problem uses the idea of sequences in a very tangible form. Children will need to recognize odd and even numbers as well as be able to count fluently both backwards and forwards. They will also have opportunities to justify their answers.

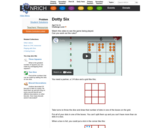
The Nrich game as introduced is intended for children who are just beginning to become confident with small numbers. However there are many variations, some suggested below, that make it suitable for older children. As with many of the NRICH games, consolidation of basic number facts is combined with an element of strategic thinking.

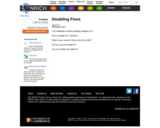
This Nrich activity provides a context for doubling multiples of 5. The children will also be noticing and describing patterns.

This team-building task is designed to develop students' team-working skills. If you wish to learn more about these skills, and find other team-builder tasks, take a look at this article.

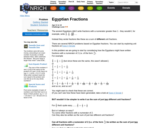
Unit fractions are the first fractions children meet, and here we discover some very surprising and interesting characteristics of these familiar numbers. Some of these characteristics were known to the ancient Egyptians whilst other conjectures are yet to be proved. Whilst meeting both old and new mathematical ideas, students can improve their fluency in addition and subtraction of fractions and be challenged to generalize and explain their findings.