In this Nrich activity students will look for patterns and options in a common everyday situation.

This Nrich problem gives children the chance to identify and continue number patterns, counting on and back in ones and twos. It is also a good chance for learners to understand the benefits of a trial and improvement approach.

In this Nrich activity students explore patterns with numbers in a square. This activity encourages multiple responses, creativity, discourse, and number sense.

This Nrich problem can be used to introduce learning about percentage increases and decreases.

Code-breaking is often about partial conclusions gradually adding up to possibilities. This problem is unlikely to be done instantly by most students, so discussion should bring up lots of helpful thoughts to share around a group, energizing explanation and stimulating individuals into new reasoning and strategy.

Students apply and interpret their understanding of area in a real world situation.

In this Nrich problem students build on their existing knowledge of proportions to build a function in an engaging context.

Countdown Fractions in this Nrich game offers a motivating context in which to practice calculating with fractions. There is usually more than one way of hitting the target, which offers an opportunity for rich discussion on the merits of alternative methods.

This Nrich activity, in line with the theme for this month, offers an 'action' to perform on a group of numbers which pupils can continue and explore. Or, you could think of the writing down of the 'description' of a sequence as an action performed on that sequence. It might particularly appeal to those pupils who enjoy number work but who are perhaps not used to succeeding in this area.

" This course covers the following topics: X-ray diffraction: symmetry, space groups, geometry of diffraction, structure factors, phase problem, direct methods, Patterson methods, electron density maps, structure refinement, how to grow good crystals, powder methods, limits of X-ray diffraction methods, and structure data bases."

This Nrich interactive environment can be used with students, perhaps on an interactive whiteboard, for many different purposes. These might include, for example, exploring ideas associated with factors and multiples, or addition and subtraction. It is also an ideal context in which to investigate fractions and ratio, or to look at finding combinations.

This Nrich problem is intentionally difficult as it stands, but this allows us to focus on promoting resilience and perseverance with children.

This problem was designed to explore equivalence of change (ie. if a 10% decrease isn't the opposite of a 10% increase, what is? ) and to move students towards the concept: exponential growth and decay.

Unit 8: Data Sets and Distributions
Lesson 8: Describing Distributions on Histograms

In this lesson, students explore various shapes and features of a distribution displayed in a histogram. They use the structure (MP7) to look for symmetry, peaks, clusters, gaps, and any unusual values in histograms. Students also begin to consider how these features might affect how we characterize a data set. For example, how might we describe what is typical in a distribution that shows symmetry? What about in a distribution that has one peak that is not symmetrical? This work is informal, but helps to prepare students to better understand measures of center and spread later in the unit. Students also distinguish between the uses and construction of bar graphs and histograms in this lesson.

'Tricks' tap into children's natural curiosity and can provide the motivation for exploring the underlying mathematics in order to unpick how they are done. This Nrich problem explores a "trick" to provide an engaging context in which to explore place value and in particular 'adding nine' as 'adding ten and subtracting one'.

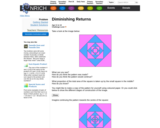
The Nrich problem offers opportunities to think about area, proportion and fractions, while offering an informal introduction to the mathematics of infinity and convergence which would not normally be met by younger students, to tempt their curiosity.

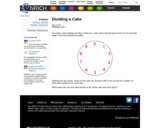
This Nrich problem gives learners practice in fractions (tenths) as well as in addition and subtraction in a challenging form.

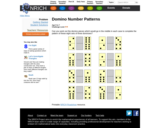
This Nrich problem uses the idea of sequences in a very tangible form. Children will need to recognize odd and even numbers as well as be able to count fluently both backwards and forwards. They will also have opportunities to justify their answers.

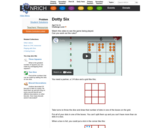
The Nrich game as introduced is intended for children who are just beginning to become confident with small numbers. However there are many variations, some suggested below, that make it suitable for older children. As with many of the NRICH games, consolidation of basic number facts is combined with an element of strategic thinking.

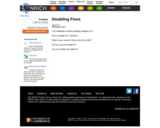
This Nrich activity provides a context for doubling multiples of 5. The children will also be noticing and describing patterns.