Conditional Remix & Share Permitted
CC BY-NC-SA
Kindergarten Eureka Math
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Assessment
- Author:
- Liberty Public Schools
- Date Added:
- 06/10/2021
Updating search results...
3633 Results
Unrestricted Use
CC BY
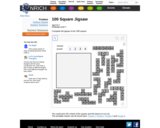
ThisNrich jigsaw a great way to reinforce children's understanding of the sequences contained within the hundred square even if they have seen it before. It could be used as an exploratory tool for children who haven't met the 0 - 99 hundred square before (puzzles 2 and 4 in the interactivity), or it could play a part in assessing their understanding of it, if they have already met it.
- Subject:
- Mathematics
- Numbers and Operations
- Material Type:
- Activity/Lab
- Interactive
- Date Added:
- 06/09/2021
Unrestricted Use
CC BY
Students will be able to celebrate the 100th day of school by bringing in a project representing it. They will also fill out a chart that has 100 blank squares for them to fill in.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Date Added:
- 05/12/2021
Unrestricted Use
CC BY
Resources to mark the 100th day of school with math activities. Challenge students to generate 100 different ways to represent the number 100. Students will easily generate 99 + 1 and 50 + 50, but encourage them to think out of the box. Challenge them to include examples from all of the NCTM Standards strands: number sense, numerical operations, geometry, measurement, algebra, patterns, data analysis, probability, discrete math, Create a class list to record the best entries. Some teachers write 100 in big bubble numeral style and then record the entries inside the numerals.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Date Added:
- 05/12/2021
Conditional Remix & Share Permitted
CC BY-NC-SA
Students will explore multi-digit numbers and the relationship between ones, tens and hundreds; a digit in one place is 10x the digit in the place to its right. Students will use their bodies to represent digits in multi-digit numbers up to the hundredths place and compare these numbers using <, =, >. Students will use their bodies as multi-digit numbers to add and subtract.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Teaching/Learning Strategy
- Date Added:
- 05/12/2021
Only Sharing Permitted
CC BY-NC-ND
To have students be able to count by multiples of 10 and comprehend the idea of a sequence of steps involved in a process.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Author:
- Carmen Blackley
- Date Added:
- 08/03/2020
Conditional Remix & Share Permitted
CC BY-SA
In this video segment from Cyberchase, the CyberSquad replaces a piece of track to get the Madre Bonita Express to the Mother's Day harvest.
- Subject:
- Mathematics
- Material Type:
- Lecture
- Author:
- U.S. Department of Education
- WNET
- Sy Hidoe
- Date Added:
- 08/04/2020
Students will examine and interpret a population chart published in 1898 — depicting changes in the makeup of the United States across time in three categories, “foreign stock,” “native stock,” and “colored” — as well as an 1893 political cartoon about immigration. Students will also explain the causes and effects of population change in the late 19th century.
- Subject:
- Mathematics
- Statistics and Probability
- Material Type:
- Activity/Lab
- Provider:
- U.S. Census Bureau
- Provider Set:
- Statistics in Schools
- Date Added:
- 11/15/2019
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: First pose the question: Here are four triangles. What do all of these triangles have in common? What makes them different from the figures that are no...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 05/24/2013
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * A copy of Grandfather Tang's Story by Ann Tompert * One set of tangrams for each student (see note in commentary) * A set of tangrams for t...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Author:
- Shereen Rasor
- Date Added:
- 05/12/2021
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * A copy of Grandfather Tang's Story by Ann Tompert * One set of tangrams for each student (see note in commentary) * A set of tangrams for t...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 05/29/2013
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials - 2 clear plastic cups for each pair of students - 4 bean seeds for each pair - soil - unifix cubes - a plant or math journal to record data ...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 04/17/2013
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials - 2 clear plastic cups for each pair of students - 4 bean seeds for each pair - soil - unifix cubes - a plant or math journal to record data ...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Author:
- Illustrative Mathematics
- Date Added:
- 08/04/2020
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * Completed monthly weather recording sheet * Crayons * Sentence strips with frames (see below) * Student worksheet Actions Every day for a m...
- Subject:
- Education
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 11/05/2013
Conditional Remix & Share Permitted
CC BY-NC-SA
Solve problems involving the four arithmetic operations with rational numbers.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Author:
- Liberty Public Schools
- Date Added:
- 06/10/2021
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials A spinner with the numbers 0, 1, 2, ... 9 A spinner with the decades 00, 10, 20, ... 90 Math journal or teacher-made worksheet Pencil Actions...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 04/19/2013
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
- Subject:
- Mathematics
- Numbers and Operations
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 02/16/2018
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
- Subject:
- Mathematics
- Numbers and Operations
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 02/16/2018
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials For each pair: * 2 ten-sided dice with the numbers 0 to 9 or two spinners with the numbers 0 to 9 * Base-10 blocks, linking cubes, or bundled...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 05/24/2013
Unrestricted Use
CC BY
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials Set of cards from 1-100, these can be purchased or created using a black marker and index cards Setup Sort the 1-100 cards into sequential gr...
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 03/16/2013