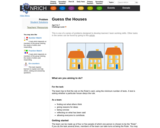
This Nrich task is a group activity or game. Students work to discover a rule by working together to evaluate patterns.
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Date Added:
- 05/31/2021

This Nrich task is a group activity or game. Students work to discover a rule by working together to evaluate patterns.

This Nrich problem provides a fraction-based challenge for students who already possess a good understanding of fraction addition and subtraction, and it leads to algebraic manipulation of that same process.

The goal of this task is to use geometry study the structure of beehives. Beehives have a tremendous simplicity as they are constructed entirely of small, equally sized walls. In order to as useful as possible for the hive, the goal should be to create the largest possible volume using the least amount of materials. In other words, the ratio of the volume of each cell to its surface area needs to be maximized. This then reduces to maximizing the ratio of the surface area of the cell shape to its perimeter.

This is course material published for a secondary Math 1 course. Authors of this work are: Scott Hendrickson, Joleigh Honey, Barbara Kuehl, Travis Lemon, Janet Sutorius and updated from the original work in 2013 in partnership with the Utah State Office of Education.
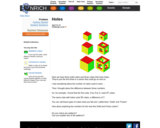
This Nrich task gives opportunities for pupils to explore, to discover, to analyze and communicate. It's a real catalyst for pupils' curiosity. It allows pupils to approach it in whatever way they find most helpful. It also provides opportunities for using and extending visualizing skills. The activity also opens out the possibility of pupils asking “I wonder what would happen if . . .?” showing their resilience and perseverance.
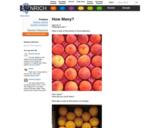
This Nrich low threshold high ceiling task is accessible to everyone. It gives children the chance to share the way they picture (visualize) numbers and their methods of counting. One of the key features of this task is that it can be interpreted differently, depending on the image, so that children can decide for themselves whether they are counting individual fruit, cartons of fruit... Therefore there may also be an opportunity for children to develop their estimation skills as well as appreciating different ways of counting.
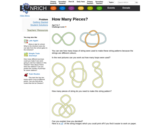
This Nrich task is designed to spark conversation about composite shapes.

This Nrich task is an unusual way to explore number patterns in a well-known context. The activity will reinforce the construction of the hundred square, and increase children's familiarity with the sequences contained within it. Using a common resource, such as a hundred square, is a good way for children to begin to use visualisation, which they may find quite difficult at first. The act of visualising in this problem tests children's understanding of how the number square is created.

In this Nrich activity students are asked to evaluate data representations based on the book "If the World Were a Village."

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use. Here are the first few lines of the commentary for this task: Each shape below has a line of symmetry. Draw a line of symmetry for each shape. Not every shape has an line of symmetry.
This Nrich problem challenges children to calculate with fractions and provides a good context in which to encourage learners to be curious about different methods of approach.
This Nrich problem uses the context of sports training to offer opportunities for learners to explore division and/or multiplication. Pupils will be required to consider the relationships between multiplication, division and fractions, which will help reveal their level of understanding.

This is the first Nrich problem in a set of three linked activities. Egyptian Fractions and The Greedy Algorithm follow on.
It's often difficult to find interesting contexts to consolidate addition and subtraction of fractions. This problem offers that, whilst also requiring students to develop and analyze different strategies and explain their findings.

This Nrich activity encourages students to notice and wonder and to engage in mathematical discussions. Students then use graphs to represent the situations.

This Nrich problem encourages children to work together to develop a method for finding a solution which will always work. It will also help to reinforce understanding of odd and even numbers.

This is an opportunity for pupils to set up their own models using a spreadsheet and investigate what happens when they change variables such as interest, inflation rates and how much is spent each year. Investigating how a small change in interest rates can affect the total income over different time periods can be enlightening. Investigating the impact of spending large amounts of money up-front can also provide valuable insights.

In this Nrich activity, students use manipulatives to investigate triangles. They are asked to construct possible triangles and to search for an impossible combination.

This is an instructional task that gives students a chance to reason about lines of symmetry and discover that a circle has an an infinite number of lines of symmetry. Even though the concept of an infinite number of lines is fairly abstract, fourth graders can understand infinity in an informal way.

This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. It is both interesting and important that these types of quadrilaterals can be distinguished by their lines of symmetry.

This task is intended for instruction, providing the students with a chance to experiment with physical models of triangles, gaining spatial intuition by executing reflections.