In this unit, children learn about attributes of shapes, compose and decompose composite shapes.

This is a second-semester graduate course on the geometry of manifolds. The main emphasis is on the geometry of symplectic manifolds, but the material also includes long digressions into complex geometry and the geometry of 4-manifolds, with special emphasis on topological considerations.

EL Education has revised the workshop model to align with the Common Core instructional shifts, embed ongoing assessment to increase responsiveness to student needs, and help students develop self-reliance and perseverance. The first component in this revised workshop (Workshop 2.0) asks students to “grapple” independently with a problem or task. The second component is a collaborative opportunity for students to be metacognitive about their own approaches, justify their mathematical reasoning, and consider others’ mathematical reasoning and thinking.

This short video and interactive assessment activity is designed to teach fourth graders about greatest common factor.

This short video and interactive assessment activity is designed to teach third graders about forming largest and smallest numbers (even and odd).

This video lesson uses the technique of induction to show students how to analyze a seemingly random occurrence in order to understand it through the development of a mathematical model. Using the medium of a simple game, Dr. Lodhi demonstrates how students can first apply the 'rules' to small examples of the game and then, through careful observation, can begin to see the emergence of a possible pattern. Students will learn that they can move from observing a pattern to proving that their observation is correct by the development of a mathematical model. Dr. Lodhi provides a second game for students in the Teacher Guide downloadable on this page. There are no prerequisites for this lesson and needed materials include only a blackboard and objects of two different varieties - such as plain and striped balls, apples and oranges, etc. The lesson can be completed in a 50-minute class period.

This Nrich problem provides a fraction-based challenge for students who already possess a good understanding of fraction addition and subtraction, and it leads to algebraic manipulation of that same process.

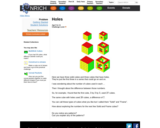
This Nrich task gives opportunities for pupils to explore, to discover, to analyze and communicate. It's a real catalyst for pupils' curiosity. It allows pupils to approach it in whatever way they find most helpful. It also provides opportunities for using and extending visualizing skills. The activity also opens out the possibility of pupils asking “I wonder what would happen if . . .?” showing their resilience and perseverance.

While learning about volcanoes, magma and lava flows, students learn about the properties of liquid movement, coming to understand viscosity and other factors that increase and decrease liquid flow. They also learn about lava composition and its risk to human settlements.

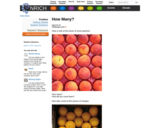
This Nrich low threshold high ceiling task is accessible to everyone. It gives children the chance to share the way they picture (visualize) numbers and their methods of counting. One of the key features of this task is that it can be interpreted differently, depending on the image, so that children can decide for themselves whether they are counting individual fruit, cartons of fruit... Therefore there may also be an opportunity for children to develop their estimation skills as well as appreciating different ways of counting.

This lesson is about the estimation of the value of Pi. Based on previous knowledge, the students try to estimate Pi value using different methods, such as: direct physical measurements; a geometric probability model; and computer technology. This lesson is designed to stimulate the learning interests of students, to enrich their experience of solving practical problems, and to develop their critical thinking ability. To understand this lesson, students should have some mathematic knowledge about circles, coordinate systems, and geometric probability. They may also need to know something about Excel. To estimate Pi value by direct physical measurements, the students can use any round or cylindrical shaped objects around them, such as round cups or water bottles. When estimating Pi value by a geometric probability model, a dartboard and darts should be prepared before the class. You can also use other games to substitute the dart throwing game. For example, you can throw marbles to the target drawn on the floor. This lesson is about 45-50 minutes. If the students know little about Excel, the teacher may need one more lesson to explain and demonstrate how to use the computer to estimate Pi value. Downloadable from the website is a video demonstration about how to use Excel for estimating Pi.

This lesson is about the estimation of the value of Pi. Based on previous knowledge, the students try to estimate Pi value using different methods, such as: direct physical measurements; a geometric probability model; and computer technology. This lesson is designed to stimulate the learning interests of students, to enrich their experience of solving practical problems, and to develop their critical thinking ability. To understand this lesson, students should have some mathematic knowledge about circles, coordinate systems, and geometric probability. They may also need to know something about Excel. To estimate Pi value by direct physical measurements, the students can use any round or cylindrical shaped objects around them, such as round cups or water bottles. When estimating Pi value by a geometric probability model, a dartboard and darts should be prepared before the class. You can also use other games to substitute the dart throwing game. For example, you can throw marbles to the target drawn on the floor. This lesson is about 45-50 minutes. If the students know little about Excel, the teacher may need one more lesson to explain and demonstrate how to use the computer to estimate Pi value. Downloadable from the website is a video demonstration about how to use Excel for estimating Pi.

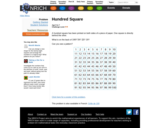
This Nrich task is an unusual way to explore number patterns in a well-known context. The activity will reinforce the construction of the hundred square, and increase children's familiarity with the sequences contained within it. Using a common resource, such as a hundred square, is a good way for children to begin to use visualisation, which they may find quite difficult at first. The act of visualising in this problem tests children's understanding of how the number square is created.

This lesson unit is intended to help you assess how students reason about geometry and, in particular, how well they are able to: use facts about the angle sum and exterior angles of triangles to calculate missing angles; apply angle theorems to parallel lines cut by a transversal; interpret geometrical diagrams using mathematical properties to identify similarity of triangles.

This short video and interactive assessment activity is designed to teach third graders an overview of reflective symmetry.

This short video and interactive assessment activity is designed to teach third graders about identifying the multiples of a given number.

Overview: This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * A copy of Grandfather Tang's Story by Ann Tompert * One set of tangrams for each student (see note in commentary) * A set of tangrams for t...
Subject: Mathematics