Students will choose the even or odd number in each question depending on what the question is asking.

The Number Pieces Basic app helps students develop a deeper understanding of place value while building their competition skills with multi-digit numbers. Students can use the number pieces to represent multi-digit numbers, count, regroup, add, and subtract. The drawing tools allow students to label representations and show their understanding numbers and math concepts.

Students will write each number in either standard form or expanded form depending on which form was presented.

Students will break down the standard form into expanded form or vice versa.

This article is for elementary teachers putting together fraction units. There is a discussion of activities and misconceptions.

Unit 6: Expressions and Equations
Lesson 13: Expressions with Exponents

In this lesson, students analyze the structure of expressions (MP7) to apply their understanding of exponents. While they practice using the notation of expressions with exponents, students recall and apply their prior understanding of operations and connect those understandings to the meaning of exponents. They write, interpret, and evaluate expressions with exponent notation where the exponents are whole numbers and the bases may be whole numbers, fractions, or decimals. Students also apply their new understanding from earlier in the unit about determining whether equations are true or false.

This learning video introduces students to the world of Fractal Geometry through the use of difference equations. As a prerequisite to this lesson, students would need two years of high school algebra (comfort with single variable equations) and motivation to learn basic complex arithmetic. Ms. Zager has included a complete introductory tutorial on complex arithmetic with homework assignments downloadable here. Also downloadable are some supplemental challenge problems. Time required to complete the core lesson is approximately one hour, and materials needed include a blackboard/whiteboard as well as space for students to work in small groups. During the in-class portions of this interactive lesson, students will brainstorm on the outcome of the chaos game and practice calculating trajectories of different equations.

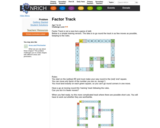
This Nrich problem will help to improve learners' knowledge of factors, especially those in the usual multiplication tables, and encourages them to use trial and improvement.

In this Nrich problem, the familiar context of sharing provides an opportunity in which to explore fractions in a variety of ways. The task involves finding fractional quantities of whole numbers as well as dividing a unit into equal pieces.

This Nrich problem starts with a simple situation which can be analyzed quickly using mental methods, but which provides a starting point for tackling a more challenging problem. The challenge can be tackled at many different levels, using trial and improvement (perhaps using spreadsheets), looking for number patterns, or with a more formal algebraic approach.

Ordering fractions can seem like quite a mundane and routine task. This Nrich problem encourages students to take a fresh look at the process of comparing fractions, and offers lots of opportunities to practice manipulating fractions in an engaging context where students can pose questions and make conjectures.

Unit 2: Introducing Ratios
Lesson 17: A Fermi Problem

This unit concludes with an opportunity for students to apply the reasoning developed so far to solve an unfamiliar, Fermi-type problem. Students must take a problem that is not well-posed and make assumptions and approximations to simplify the problem (MP4) so that it can be solved, which requires sense making and perseverance (MP1). To understand what the problem entails, students break down larger questions into more-manageable sub-questions. They need to make assumptions, plan an approach, and reason with the mathematics they know.

Unit 9: Putting It All Together
Lesson 1: Fermi Problems

This lesson is optional. The activities in this lesson plan are sometimes called “Fermi problems” after the famous physicist Enrico Fermi. A Fermi problem requires students to make a rough estimate for quantities that are difficult or impossible to measure directly. Often, they use rates and require several calculations with fractions and decimals, making them well-aligned to grade 6 work. Fermi problems are examples of mathematical modeling (MP4), because one must make simplifying assumptions, estimates, research, and decisions about which quantities are important and what mathematics to use. They also encourage students to attend to precision (MP6), because one must think carefully about how to appropriately report estimates and choose words carefully to describe the quantities.

Each of these activities can stand on its own. If students do the first before the second, the second will take less time. It is very likely that it would take more than a single day to do all of the activities in this lesson. One option is to let students choose an activity that interests them. If you choose to conduct the lesson in this manner, begin by posing these scenarios, one for each activity in this lesson, to students:

“Imagine that an ant ran from Los Angeles to New York City.”
“Imagine a warehouse that has a rectangular floor and contains all of the boxes of breakfast cereal bought in the United States every year.”
“Imagine that the entire Washington Monument had to be completely retiled.”
Then ask:

“Which one interests you the most? Why?”
“What questions could we ask about each situation?”
“What information would you want to know in order to investigate that particular situation?”
Each student or group can explore the problem that interests them the most and share their findings.

As with all lessons in this unit, all related standards have been addressed in prior units; this lesson provides an optional opportunity to go more deeply and make connections between domains.

Unit 3: Unit Rates and Percentages
Lesson 15: Finding This Percent of That

Students have practiced solving three different types of percentage problems (corresponding to finding A, B, or C respectively when A% of B is C). This lesson focuses on finding “A% of B” as efficiently as possible. While the previous lesson used numbers that students could calculate mentally, the numbers in this lesson are purposefully chosen to be difficult for students to calculate mentally or to represent on a double number line diagram, so as to motivate them to find the simplest way to do the calculation by hand.

The third activity hints at work students will do in grade 7, namely finding a constant of proportionality and writing an equation to represent a proportional relationship.

This video is part of the Learn and Grow with WHRO TV series. Watch Alystra Barefoot teach about setting up a learning journal.

Unit 8: Data Sets and Distributions
Lesson 10: Finding and Interpreting the Mean as the Balance Point

In the previous lesson, students interpreted the mean as a fair-share value—i.e., what each group member would have if all the values are distributed such that all members have the same amount. In this lesson, students use the structure of the data (MP7) to interpret the mean as the balance point of a numerical distribution. They calculate how far away each data point is from the mean and study how the distances on either side of the mean compare.

Students connect this interpretation to why we call the mean a measure of the center of a distribution and, through this interpretation, begin to see how the mean is useful in characterizing a “typical” value for the group. Students continue to practice calculating the mean of a data set (MP8) and interpreting it in context (MP2).

Area Builder is an interactive website that allows students to build shapes to find the area and the perimeter. There are two-parts for students to use, the explore and the game. The first allows for exploration while building, the second is a game that has them figuring out the area and the perimeter. There are 6 levels.

Unit 3: Unit Rates and Percentages
Lesson 16: Finding the Percentage

While students have found percentages with easy numbers before now, in this lesson they will develop a general structure (MP7) that will work for any numbers.

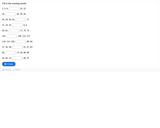
Students will be able to calculate the missing number by identifying the pattern of numbers.