Squares_ywQlIf1.pngThis image is a row of six boxes where learners can use this image to solve the word problem.
Eureka math
This lesson uses tall tale read alouds to reinforce the common elements, or text structure, of tall tales. As the text is read aloud, students examine the elements of the book that are characteristic of tall tales. Then using what they've learned, they write and perform tall tales of their own.
This unit on thermal energy transfer begins with students testing whether a new plastic cup sold by a store keeps a drink colder for longer compared to the regular plastic cup that comes free with the drink. Students find that the drink in the regular cup warms up more than the drink in the special cup. This prompts students to identify features of the cups that are different, such as the lid, walls, and hole for the straw, that might explain why one drink warms up more than the other.
Students investigate the different cup features they conjecture are important to explaining the phenomenon, starting with the lid. They model how matter can enter or exit the cup via evaporation However, they find that in a completely closed system, the liquid inside the cup still changes temperature. This motivates the need to trace the transfer of energy into the drink as it warms up. Through a series of lab investigations and simulations, students find that there are two ways to transfer energy into the drink: (1) the absorption of light and (2) thermal energy from the warmer air around the drink. They are then challenged to design their own drink container that can perform as well as the store-bought container, following a set of design criteria and constraints.
This unit on weather, climate, and water cycling is broken into four separate lesson sets. In the first two lesson sets, students explain small-scale storms. In the third and fourth lesson sets, students explain mesoscale weather systems and climate-level patterns of precipitation. Each of these two parts of the unit is grounded in a different anchoring phenomenon.
The unit starts out with anchoring students in the exploration of a series of videos of hailstorms from different locations across the country at different times of the year. The videos show that pieces of ice of different sizes (some very large) are falling out of the sky, sometimes accompanied by rain and wind gusts, all on days when the temperature of the air outside remained above freezing for the entire day. These cases spark questions and ideas for investigations, such as investigating how ice can be falling from the sky on a warm day, how clouds form, why some clouds produce storms with large amounts of precipitation and others don’t, and how all that water gets into the air in the first place.
The second half of the unit is anchored in the exploration of a weather report of a winter storm that affected large portions of the midwestern United States. The maps, transcripts, and video that students analyze show them that the storm was forecasted to produce large amounts of snow and ice accumulation in large portions of the northeastern part of the country within the next day. This case sparks questions and ideas for investigations around trying to figure out what could be causing such a large-scale storm and why it would end up affecting a different part of the country a day later.
This Nrich problem is a good, yet simple, activity that can get pupils thinking hard about numerals, numbers and place value. It also provides a context for discussing different ways of recording and for encouraging systematic working.
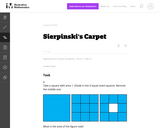
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Take a square with area 1. Divide it into 9 equal-sized squares. Remove the middle one. What is the area of the figure now? Take the remaining 8 square...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
Create and evaluate expressions involving variables and whole number exponents.
b. Evaluate expressions at specific values of the variables.
d. Write and evaluate algebraic expressions.
Solve one-step equations
Solve one-step linear equations in one variable involving non-negative rational numbers.
*(guaranteeing only whole numbers)
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: A penny is about $\frac{1}{16}$ of an inch thick. In 2011 there were approximately 5 billion pennies minted. If all of these pennies were placed in a s...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: A penny is about $\frac{1}{16}$ of an inch thick. In 2011 there were approximately 5 billion pennies minted. If all of these pennies were placed in a s...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Anna enjoys dinner at a restaurant in Washington, D.C., where the sales tax on meals is 10%. She leaves a 15% tip on the price of her meal before the s...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: What is the last digit of $7^{2011}$? Explain. What are the last two digits of $7^{2011}$? Explain....
Find the area of polygons by composing or decomposing the shapes into rectangles or triangles.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The vertices of eight polygons are given below. For each polygon: * Plot the points in the coordinate plane connect the points in the order that they a...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.